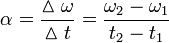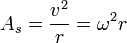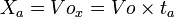Kumpulan Rumus Kimia Lengkap Beserta Penjelasan
Kumpulan Rumus Kimia Lengkap Beserta Penjelasan,
dalam dunia pelajaran untuk mengetahui suatu unsur biasanya kita
menggunakan suatu rumus, dan jika di mata pelajaran kimia ada beberapa
rumus untuk beberapa molekul seperti Rumus untuk Molekuk Monoatomik, Rumus Untuk Molekuk Diatomik, Poliatomik dan lai lain.
Rumus kimia adalah rumus yang menyatakan lambang atom dan jumlah atom unsur yang menyusun senyawa. Rumus kimia disebut juga rumus molekul, karena penggambaran yang nyata dari jenis dan jumlah atom unsur penyusun senyawa yang bersangkutan.
Rumus kimia adalah rumus yang menyatakan lambang atom dan jumlah atom unsur yang menyusun senyawa. Rumus kimia disebut juga rumus molekul, karena penggambaran yang nyata dari jenis dan jumlah atom unsur penyusun senyawa yang bersangkutan.
Berbagai bentuk rumus kimia sebagai berikut:
1. Rumus kimia untuk molekul unsur monoatomik.
Rumus kimia ini merupakan lambang atom unsur itu sendiri.
Contoh : Fe, Cu, He, Ne, Hg.
2. Rumus kimia untuk molekul unsur diatomik.
Rumus kimia ini merupakan penggabungan dua atom unsur yang sejenis dan saling berikatan.
Contoh : H2, O2, N2, Cl2, Br2, I2.
3. Rumus kimia untuk molekul unsur poliatomik.
Rumus kimia ini merupakan penggabungan lebih dari dua atom unsur yang sejenis dan saling berikatan.
Contoh : O3, S8, P4.
4. Rumus kimia untuk molekul senyawa ion
Merupakan rumus kimia yang dibentuk dari penggabungan antar atom yang bermuatan listrik, yaitu ion positif (kation) dan ion negatif (anion). Ion positif terbentuk karena terjadinya pelepasan elektron (Na+, K+, Mg2+), sedangkan ion negatif terbentuk karena penangkapan elektron (Cl-, S2-, SO42-).
Penulisan rumus kimia senyawa ion sebagai berikut.
-Penulisan diawali dengan ion positif (kation) diikuti ion negatif (anion).
-Pada kation dan anion diberi indeks, sehingga didapatkan senyawa yang bersifat netral (jumlah muatan (+) = jumlah muatan (-)).
-Bentuk umum penulisannya sebagai berikut.
Contoh :
Na+ dengan Cl- membentuk NaCl.
Mg2+ dengan Br- membentuk MgBr2.
Fe2+ dengan SO42- membentuk FeSO4.
5. Rumus kimia untuk senyawa biner nonlogam dengan nonlogam.
Penulisan rumus kimia ini berdasarkan kecenderungan atom yang bermuatan positif diletakkan di depan, sedangkan kecenderungan atom bermuatan negatif diletakkan di belakang menurut urutan atom berikut ini.
B � Si � C � S � As � P- N � H � S � I � Br � Cl � O � F
Contoh : CO2, H2O, NH3.
6. Rumus kimia /rumus molekul senyawa organik.
Rumus ini juga menunjukkan jenis dan jumlah atom penyusun senyawa organik yang berdasarkan gugus fungsi masing � masing senyawa.
Contoh :
CH3COOH : asam asetat
CH4 : metana (alkana)
C2H5OH : etanol (alkohol)
7. Rumus kimia untuk senyawa anhidrat.
Anhidrat merupakan sebutan dari garam tanpa air kristal (kehilangan molekul air kristalnya) atau H2O.
Contoh :
CaCl2 anhidrous atau CaCl2.2H2O.
CuSO4 anhidrous atau CuSO4.5H2O.
8. Rumus kimia untuk senyawa kompleks.
Penulisan rumus senyawa dan ion kompleks ditulis dalam kurung siku [...].
Contoh :
Na2[MnCl4]
[Cu(H2O)4](NO3)2
K4[Fe(CN)6]
RUMUS EMPIRIS
Rumus empiris merupakan rumus kimia yang menyatakan jenis dan perbandingan paling sederhana (bilangan bulat terkecil) dari atom � atom penyusun senyawa.
Contoh :
C12H22O11 (gula)
CH2O (glukosa)
C2H6O (alkohol)
CHO2 (asam oksalat)
RUMUS STRUKTUR
Rumus struktur merupakan rumus kimia yang menggambarkan posisi atau kedudukan atom dan jenis ikatan antar atom pada molekul.
Rumus struktur secara singkat dituliskan :
CH3CH3
CH3COOH
RUMUS BANGUN/BENTUK MOLEKUL
Adalah rumus kimia yang menggambarkan kedudukan atom secara geometri/ tiga dimensi dari suatu molekul.



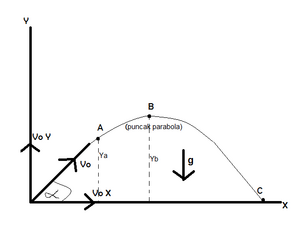
 = Jarak yang ditempuh (m, km)
= Jarak yang ditempuh (m, km)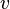 = Kecepatan (km/jam, m/s)
= Kecepatan (km/jam, m/s) = Waktu tempuh (jam, sekon)
= Waktu tempuh (jam, sekon) .
. .
.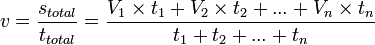



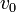 = Kecepatan awal (m/s)
= Kecepatan awal (m/s) = Kecepatan akhir (m/s)
= Kecepatan akhir (m/s)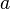 = Percepatan (m/s2)
= Percepatan (m/s2)
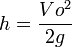
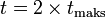

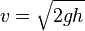
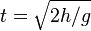
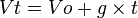
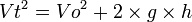
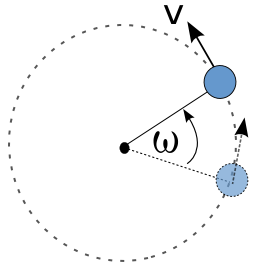
 sekon, maka benda dikatakan melakukan perpindahan sudut.
sekon, maka benda dikatakan melakukan perpindahan sudut. atau keliling lingkaran. Besar perpindahan sudut dalam 1 putaran penuh adalah
atau keliling lingkaran. Besar perpindahan sudut dalam 1 putaran penuh adalah 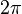 radian atau 360°.
radian atau 360°.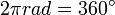


 = perpindahan sudut (rad)
= perpindahan sudut (rad) = kecepatan sudut (rad/s)
= kecepatan sudut (rad/s) ): perpindahan sudut per selang waktu.
): perpindahan sudut per selang waktu.
 ): perubahan kecepatan sudut per selang waktu.
): perubahan kecepatan sudut per selang waktu.